여러가지 평균에 대해서 알아봤는데요, 이번엔 데이터의 분산과 변수의 관련성에 대해서 알아보겠습니다.
이를 알아보는 이유는 평균만으로는 데이터가 어떻게 흩어져 있는지 모르기 때문입니다.
따라서 최댓값, 최솟값, 분위수, 사분위 범위, 분산(표준편차) 등의 지표를 이용하여 데이터의 흩어진 정도를 파악합니다.
분위수
n개의 데이터를 작은 순서대로 나열해 놓고, 그것을 k등분 했을 때 경계가 되는 수를 분위수라고 합니다.
4분위수를 가장 많이 쓰는데, 2분위수는 중앙값이라고도 합니다.
사분위 범위
제 3사분위수와 제 1사분위수의 차를 말합니다 데이터가 중앙값 주위에 집중될수록 사분위 범위는 작아집니다.
분산
$s^{2} = \left \{ (x_{1}-\bar{x})^{2}+(x_{1}-\bar{x})^{2}+\cdots +(x_{1}-\bar{x})^{2} \right \}\div n = \frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}$
이상치
데이터의 평균에서 멀리 떨어져 있는 값을 이상치라고 합니다.
변동계수
두 개의 데이터가 흩어진 정도를 비교하는 경우에 사용합니다.
변동계수는 표준편자를 평균으로 나눈 값입니다.
상관 계수
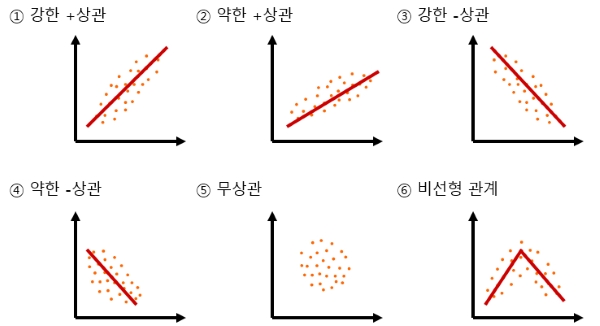
두 변수 사이에서 상정되는 '한쪽이 증가하면 다른쪽도 증가한다', '한쪽이 증가하면 다른쪽은 감소한다'와 같은 직선적인 관계를 상관이라고 합니다.
피어슨의 적률상관계수
상관의 정도를 나타내는 -1에서 1 사이의 값을 취합니다.
변수 x와 y의 상관계수 r는 다음과 같이 계산합니다.
$r = \frac{(x_{1}-\bar{x})(y_{1}-\bar{y})+(x_{2}-\bar{x})(y_{2}-\bar{y})+\cdots +(x_{n}-\bar{x})(y_{n}-\bar{y})}{\sqrt{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots +(x_{n}-\bar{x})^{2}}\sqrt{(y_{1}-\bar{y})^{2}+(y_{2}-\bar{y})^{2}+\cdots +(y_{n}-\bar{y})^{2}}}$
r이 1에 가까우면 양의 상관이 강해집니다.
<한쪽이 증가하면 다른 쪽이 증가한다>
r이 -1에 가까우면 음의 상관이 강해집니다.
<한쪽이 증가하면 다른 쪽이 감소한다>
r이 0에 가까우면 상관이 없습니다.
<산포도 상 점은 원을 그린다>
순위상관
순위 데이터밖에 사용할 수 없는 경우나 두 변수 간에 곡선적인 관계가 상정되는(산포도 모양이 곡선이 되는) 경우는 순위상관계수를 이용합니다.
스피어만의 순위상관계수
순위 데이터에 대해 계산한 피어슨의 확률상관계수가 스피어만의 순위상관계수입니다.
연속변수일 경우는 먼저 순위 데이터로 변환합니다.
켄달의 순위상관계수
x에 대한 순위와 y에 대한 순위가 일치하는지의 여부에 주목해서 상관의 정도를 측정하는 지표입니다.
소비자 1의 순위 데이터(x1, y1)과 소비자 2의 순위 데이터(x2, y2)에 대해
1) x1 < x2 이고 y1 < y2 일 때(부등호의 방향이 같을 때) -> 순위의 일치
2) x1 < x2 이고 y1 > y2 일 때(부등호의 방향이 다를 때) -> 순위의 불일치
순위가 일치하는 경우의 수를 A, 불일치하는 경우의 수를 B, 데이터 쌍의 수를 n이라 할 때
켄달의 순위상관계수 t(타우)는 다음 식으로 계산할 수 있습니다.
$\tau = \frac{(A-B)}{_{n}C_{2}}$
'데이터 과학 > 통계학도감' 카테고리의 다른 글
| 확률분포2 [ 통계학도감5 ] (0) | 2019.10.17 |
|---|---|
| 확률분포1 [ 통계학도감4 ] (0) | 2019.10.15 |
| 기술통계학1 [ 통계학도감2 ] (0) | 2019.10.02 |
| 통계학이란 [ 통계학도감1 ] (0) | 2019.09.25 |
| 2학기 공업일반 계획 (0) | 2019.08.15 |



